Center for Financial Innovation and Stability

Notes from the Vault
Nikolay Gospodinov and Ibrahim Jamali
March 2019

"Carry" is broadly defined as the expected return on an asset by holding its price fixed, and can be constructed as a (scaled) spread variable for any asset class. A currency carry involves borrowing in a low-interest currency and simultaneously investing in a high-interest currency; bond carry is essentially the (roll-down) adjusted term spread; and equity (commodity) carry is the expected dividend (convenience) yield in excess of the risk-free rate. In addition to revisiting the performance of carry as an investment strategy in various asset markets, this post highlights the predictive power of the bond and commodity carry for macroeconomic variables as well as its informational content for studying the common factor structure within and across asset classes.

Investment strategies that exploit profit opportunities in the carry—called carry trades—have traditionally provided investors, despite occasional crashes, with sustained returns and profits. While the currency carry trade has attracted significant attention (Burnside et al., 2011; see also here), existing research also establishes that carry-based investment strategies are profitable in the commodity markets (Szymanowska et al., 2014) as well as across other asset classes (Koijen et al., 2018). Chart 1 plots the cumulative returns to currency and commodity carry trade compared with that on the S&P 500 stock index for the period January 2000 to December 2017.

With evidence-based factor investing—as well as smart beta investing—increasingly in vogue, carry-based investment strategies now constitute an integral component of the factor investing toolbox that market participants employ. The success of the carry strategies has led hedge funds and active asset managers to exploit the advantages of a diversified investment strategy, which combines carry with more traditional factors, such as momentum and value, to generate superior profits (see here and here).

Despite the widespread interest in the profitability of carry-based investment strategies, the informational content arising from the forward-looking nature of the carry has received only limited attention. The predictive power of interest rate spreads and commodity convenience yields for forecasting recessions and inflation, respectively, as well as usefulness of exchange rate movements for eliciting information about the future stance of the global monetary policy have been documented in isolation and not directly linked to their essential carry structure. Furthermore, the unified construction of carry allows for studying the existence of a common carry factor structure across asset classes. In this post, we highlight the appealing characteristics of the carry for investment and policy analysis and outline some directions for future research.

The next section provides a generic definition of carry and discusses some underlying fundamental principles in the construction of carry across asset markets in order to build an intuition about the appeal of carry for investment and economic analysis. Readers who are not interested in the technical details can skip to the empirical section about the economic significance of carry.

Construction of carry
Carry is a characteristic of any asset and can be constructed from futures (or forward) and spot price data as (Koijen et al., 2018):

where S_t is the spot price and F_t is a futures contract with one period (e.g., month) to expiration. As we will see later, this definition could involve a multi-period futures contract that underlies the forward-looking nature of the carry factor.

To gain some intuition about the economic content of the carry factor, it would be instructive to discuss this within the context of commodity pricing. In the commodity markets, the cost-of-carry model (Fama and French, 1988) provides a no-arbitrage relation between futures and spot prices that implicitly defines a convenience yield (also known as an interest-adjusted basis), which measures the benefits accruing to the holder of the physical commodity. To illustrate this, suppose that an investor simultaneously assumes a long spot and an offsetting short positon in a commodity futures contract with the return on the long leg is where denotes the convenience yield from holding the commodity, and the return on the short leg is given by 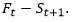The total return from this long/short position, is non-stochastic and it must, by the absence of arbitrage, equal the return from investing at the risk-free rate From this no-arbitrage condition, it follows that the convenience yield can be obtained as

Furthermore, substituting for in equation (1) implies that the commodity carry (abstracting from storage costs) is given by the convenience yield in excess of the risk-free rate:

In practice, reliable spot prices may not be available or a futures contract with exactly one month to expiration may not be traded on the futures exchange. More generally, the availability of spot and futures prices at different maturities can vary across different assets, which may hamper the empirical analysis. Thus, it would be beneficial to construct consistent measures of the carry across different assets.¹

In the foreign exchange market, the covered interest parity provides the no-arbitrage relation binding futures (forward) to spot prices:

where are the domestic and foreign interest rates, respectively, on similar securities. Plugging this expression for in the definition for carry (eq. (1)) yields

implying that the currency carry is the discounted interest rate spread across countries. Given the availability of spot price data for the currency markets, the currency carry can be constructed from spot price data and a synthetic one-month futures price obtained by linear interpolation between the two nearest futures contracts.

In line with the construction of carry for commodity and currency markets, the bond carry is also a scaled version of the forward-spot spread. More specifically, the bond carry at maturity n is the slope of the yield curve adjusted for price increases as the bond rolls down the yield curve or

where is the implied forward rate of zero-coupon bonds with n-1 and n periods to maturity. That is, the bond carry is the discounted interest rate (forward) spread across maturities.²

One interesting example where the carry constitutes a significant portion of the observed bond yield is for Treasury inflation-protected securities (TIPS) that are indexed to the nonseasonally adjusted consumer price index (CPI-U).³ TIPS carry is generated by the accredited principal tied to the nonseasonally adjusted CPI-U. Because TIPS yields are routinely used as a measure for real yields and market-implied inflation compensation (breakeven inflation), the existence of carry could potentially obfuscate, if not properly isolated, their analysis. Carry, computed again as the spread between the forward and spot yields, could be substantial at shorter-term maturities, but it gradually declines with the maturity of the bond. The strong seasonality of the TIPS yields is reported in a previous Atlanta Fed macroblog post. Financial shocks (for example, oil price shocks) can exacerbate negative carry or dampen the positive carry. Since TIPS are relatively less attractive to investors when carry is negative, this could be confused with a genuine movement in real yields or inflation compensation.

Economic significance of carry
Carry provides a convenient framework for characterizing the common factor structure across asset classes. From a theoretical point of view, it offers a unified framework for constructing and modeling a common primitive object across assets. When studied in isolation, the literature on modeling different assets often uses different primitive objects of analysis: returns (for equity), yields (for bonds), prices (for commodities), and so on. From a statistical perspective, these different primitive objects have widely different persistence properties that makes their joint analysis quite challenging. Even when we construct returns for all asset classes, the lack of persistence and the highly volatile nature of returns make them a less than ideal primitive process for extracting common signals within and across asset classes.

Carry factors, on the other hand, are characterized with persistence in the middle of the spectrum—persistent but still mean-reverting processes—that provide a closer statistical match to the observed variations in the macro series such as annualized GDP growth and inflation. Because carry is constructed as a spread between spot and futures prices, it stabilizes the dynamics of the series by removing concurrent outliers and noise in the price series and creates a primitive process with "homogeneous" persistent properties across assets. Furthermore, unlike financial prices and yields, the lack of extreme persistence in carry helps to sidestep nonstandard inference issues that arise in the analysis of near nonstationary variables. At the same time, the stronger serial dependence than in returns proves beneficial when extracting slow-moving signals from various assets. Finally, we want to stress again the forward-looking nature of carry embedded in the futures prices. Below, we demonstrate the predictive power of carry for inflation and real economic activity as well as its informational content about co-movements in the international markets.

Since the late 1980s, a sizable literature has examined the predictive power of several interest rate spreads for predicting the start (but not necessarily the severity or duration of) recessions; some recent contributions can be found here, here, here, and in a macroblog post by Atlanta Fed president Raphael Bostic. Although some of the inference suffers from hindsight and data mining bias, the evidence points to the term spread as a robust warning indicator of near-future economic downturns and possible recessions. Since bond carry is essentially an adjusted term spread, it is not surprising that it contains similar information. Instead of choosing one particular term spread, we average the bond carry across all quarterly (1 to 40 quarters) maturities for the period from the second quarter of 1961 to the first quarter of 2019. This provides some "insurance" against the possibility that the predictive ability of individual spreads changes over time. The average bond carry is plotted in chart 2 where the shaded areas signify National Bureau of Economic Research-dated recessions. Interestingly, unlike several popular term spreads, the bond carry does not produce any false positives (such as incorrectly predicting a recession) over the whole sample. Despite this, the seemingly good predictive power of bond carry also suffers from in-sample hindsight biases and a small number of effective observations (seven recessions).

The second example involves the use of the commodity carry for forecasting U.S. core inflation. Gospodinov and Ng (2013) have documented the strong (in- and out-of-sample) predictive power of commodity convenience yields for headline and core inflation. The source of this forecasting was traced to the ability of carry-type measures to encompass information about future global and domestic excess demand. Gospodinov's Atlanta Fed working paper (2016) provided further evidence of the impressive forecasting power of a simple aggregate of a small number of commodity carry proxies for the consumer price index core inflation that is stripped from the food and energy components. This suggests that aggregated, forward-looking information embedded in commodity carry can inform policymakers and market participants about the future dynamics of the underlying inflation trends. The benefits of this predictive information are further enhanced by the real-time, high-frequency availability of futures commodity prices and carry. Chart 3 presents the average carry factor (lagged 12 months) and the actual one-year CPI core inflation over the period January 2000 to February 2019. The plot is revealing about the strong, one-year-ahead predictive relationship between the commodity carry and core inflation (with a correlation coefficient of 68 percent).

Finally, we present results on some strong commonalities in currency carry that are not that evident from exchange rate levels or currency returns. Using spot and (synthetic) one-month futures data on the Japanese yen (JPY), Canadian dollar (CAD), Australian dollar (AUD), Swiss franc (CHF), Euro (EUR), and British pound (GBP) against the U.S. dollar (USD), we construct the currency carry for each currency and extract a common carry factor via principal components from the standardized data. Chart 4 plots the individual carry factors (left axis) and the estimated common component (right axis) for the period from May 1998 to December 2017.

As evident from chart 4, there is substantial commonality in the currency carry (with correlations between the individual series and the common factor ranging from 59 percent to 89 percent). This commonality may not be very surprising given that the U.S. dollar is the base currency for all these carry factors, but that is not immediately obvious from examining the exchange rate levels or returns. It is interesting to link this within-asset common variation with bond and commodity carry. We are currently developing a similar, but more comprehensive, approach for using carry in characterizing the common factor structure across asset classes.

Conclusion
This post outlines the profitability of carry-based investment strategies in the currency and commodity markets, highlights the informational content of carry factors for policy analysis, and documents the commonality in the currency carry. Because carry factors are persistent but still mean-reverting, their statistical properties are aligned with those of key macroeconomic variables such as year-over-year output growth and inflation, thus making them potentially useful predictors. Indeed, the evidence presented in this post suggests that the bond and commodity carry appear to be robust predictors of recessions and core inflation, respectively.

The findings presented in this post have important implications for policymaking and portfolio management. From a policymaking perspective, carry factors could hold significant promise for predicting business cycle dynamics and inflation. On the portfolio management front, the commonality in carry factors could be useful for a more complete and unified understanding of the drivers of the cross-section of returns across asset classes. This is a promising avenue for research that the authors continue to explore.

References

Burnside, Craig, Martin Eichenbaum, and Sergio Rebelo (2011). "Carry Trade and Momentum in Currency Markets." Annual Review of Financial Economics 3, 511-535. Available behind a paywall at: https://www.annualreviews.org/doi/abs/10.1146/annurev-financial-102710-144913

Fama, Eugene F., and Kenneth R. French (1988). "Business Cycles and the Behavior of Metals Prices." Journal of Finance 43, 1075-1093. Available behind a paywall at: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1540-6261.1988.tb03957.x.

Gospodinov, Nikolay (2016). "The Role of Commodity Prices in Forecasting U.S. Core Inflation." Atlanta Fed Working Paper 2016-5.

Gospodinov, Nikolay, and Serena Ng (2013). "Commodity Prices, Convenience Yields, and Inflation." Review of Economics and Statistics 95, 206-219. Available behind a paywall at: https://www.mitpressjournals.org/doi/abs/10.1162/rest_a_00242.

Koijen, Ralph S. J., Tobias J. Moskowitz, Lasse Heje Pedersen, and Evert B. Vrugt (2018). "Carry." Journal of Financial Economics 127, 197-225. Available behind a paywall at: https://www.sciencedirect.com/science/article/pii/S0304405X17302908.

Szymanowska, Marta, Frans De Roon, Theo Nijman, and Rob Van Den Goorbergh (2014). "An Anatomy of Commodity Futures Risk Premia." Journal of Finance 69, 453-482. Available behind a paywall at: https://onlinelibrary.wiley.com/doi/abs/10.1111/jofi.12096.

Nikolay Gospodinov is a financial economist and senior adviser at the Atlanta Fed. Ibrahim Jamali is an associate professor of finance at the Olayan School of Business of the American University of Beirut. The views expressed here are the authors' and not necessarily those of the Federal Reserve Bank of Atlanta or the Federal Reserve System. If you wish to comment on this post, please email atl.nftv.mailbox@atl.frb.org.

_______________________________________

¹ For commodity markets, for example, a synthetic spot price can be computed using the nearest two futures contracts by extrapolating the futures curve. Similarly, a synthetic one-month futures price can be constructed by linear interpolation between the two nearest futures contracts.

² For details concerning the construction of equity, options, and other assets' carry, see (Koijen et al., 2018).

³ The TIPS market is a relatively large (with an outstanding amount of approximately 10 percent of that for nominal Treasuries) but concentrated (with 10 percent held in the Fed's System Open Market Account or SOMA portfolio and another 10 percent to 12 percent held by the top two or three bond funds) market with a number of specificities that are believed to contaminate the observed TIPS yields. These include an indexation lag, deflation floor, tenor-specific liquidity, taxation of "phantom" income (taxation on annual increases in a bond's principal even though this principal is not paid until maturity), and so forth.